| Previous | Table of Contents | Next |
Denormalizing Many-To-Many Data Relationships
In many cases, a many-to-many relationship can be condensed into a more efficient structure to improve the speed to data retrieval. After all, less tables need to be joined to get the desired information. To understand how a many-to-many relationship can be collapsed into a more compact structure by considering the relationship between a course and a student, refer to Figure 1.13.
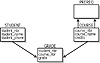
Figure 1.13 An example university database.
A student takes many courses, and each course has many students. This is a classical many-to-many relationship and requires that we define a junction table between the base entities to establish the foreign keys necessary in joining them together. Note that the junction table is called GRADE with the following contents: course_nbr, the primary key for the COURSE table; student_nbr, the primary key for the STUDENT table; and grade, which is a no-key attribute to both foreign keys. Next, consider the question, “In what context does a grade have meaning?” Stating “The grade was A in CS-101” is insufficient, and stating “Joe earned an A” makes no sense. Only when both the student number and the course number are associated does the grade column have meaning. Stating “Joe earned an A in CS-101” does make sense.
Dealing With Recursive Data Relationships
Recursive many-to-many relationships contain an object that also has a many-to-many relationship with other occurrences of the same object. These relationships are often termed Bill-of-Materials (BOM) relationships, and the graphical representation of the recursive relationship is sometimes termed a Bill-of-Materials explosion. These relationships are termed recursive because a single query makes many subpasses through the tables to arrive at the solution (see Figure 1.14).

Figure 1.14 An example of recursive many-to-many relationships.
Bill-of-Materials relationships denote an object with a many-to-many relationship with another object in the same class. For example, a part may consist of other parts, but at the same time it is a component in a larger assembly. A class at a university may have many prerequisites, but at the same time it is a prerequisite for another class. In the legal arena, a court case may cite other cases—but at the same time it is being cited by later cases.
For example, a BOM request for components of a Big Meal shows that it consists of a hamburger, fries, and soda. Yet a hamburger consists of a meat patty, bun, and pickle—and a meat patty consists of meat and filler, and so on. Another example of a BOM relationship would be the division of a carburetor into subparts, although the carburetor itself is a subassembly in a still larger unit, such as an engine.
Figure 1.15 describes course-prerequisite hierarchy for a university. Note that the Is-a prerequisite relationships are relatively straightforward, indicating which courses are required before taking another course. For example, the prerequisites for Linear Equations 445 are Business 400, Accounting 305, and Multivariate Statistics 450. These courses all have prerequisites of their own, which may also have prerequisites, and so on.

Figure 1.15 Viewing a recursive many-to-many relationship as an ordinary many-to-many relationship.
Each occurrence of a COURSE object has different topics, and a complete implementation must iterate through all courses until reaching terminus, the point where the course has no further prerequisites.
Unfortunately, the recursive many-to-many relationship is very confusing and almost impossible to understand without the aid of a graphical representation. Visualize the recursive many-to-many relationship as an ordinary many-to-many relationship with the owner entity “pulled apart” into owner1 and owner2. Figure 1.15 shows how the junction entity establishes the relationship.
Only graphical representations conceptualize a recursive many-to-many relationship. In the CODASYL model, these are called “set occurrence” diagrams, and they show the pointer chains that link the relationships (see Figure 1.16). Table sketches show that the junction table contains both an implosion and an explosion column in relational databases. Use the set occurrence diagram to understand data relationships.
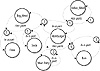
Figure 1.16 A set occurrence diagram for a recursive relationship.
In Figure 1.16, we can navigate the database, determining the components for a Big_Meal. To navigate this diagram, start at the object Big_Meal and follow the Has_parts link to the bubble containing the number 1. This is the quantity for the item. We now follow these bubbles to the Is_a_part link, which shows that one order of fries is included in a Big_Meal. We return to the Has_parts link for Big_Meal and find the next bubble. The Is_a_part link shows that one soda is included in a Big_Meal. We then continue this process until no further entities can be found in the Has_parts relationship. In sum, the Has_parts relationships indicate that a Big_Meal consists of one order of fries, one soda, and one hamburger. In addition, the hamburger consists of two meat patties and one bun.
Here we can see how the database is navigated to determine which parts use a specific component. For example, if you start at the Hamburger bubble and navigate the Is_a_part relationships, you see that one hamburger participates in the Value_Meal and also in the Big_Meal.
Recursive relationships can now be generated from the structure. For example, when listing the components of a Big_Meal, all components appear as in Table 1.2.
| Part 1 | Part 2 | Part 3 | Quantity |
|---|---|---|---|
| Hamburger | 1 | ||
| Meat Patty | 2 | ||
| Oatmeal | 4 oz. | ||
| Beef Lips | 3 oz. | ||
| Bun | 1 | ||
| Fries | 1 order | ||
| Potato | 1 | ||
| Grease | 1 cup | ||
| Soda | 1 | ||
| Ice | 1/2 cup | ||
| Drink | 1/3 cup |
| Previous | Table of Contents | Next |